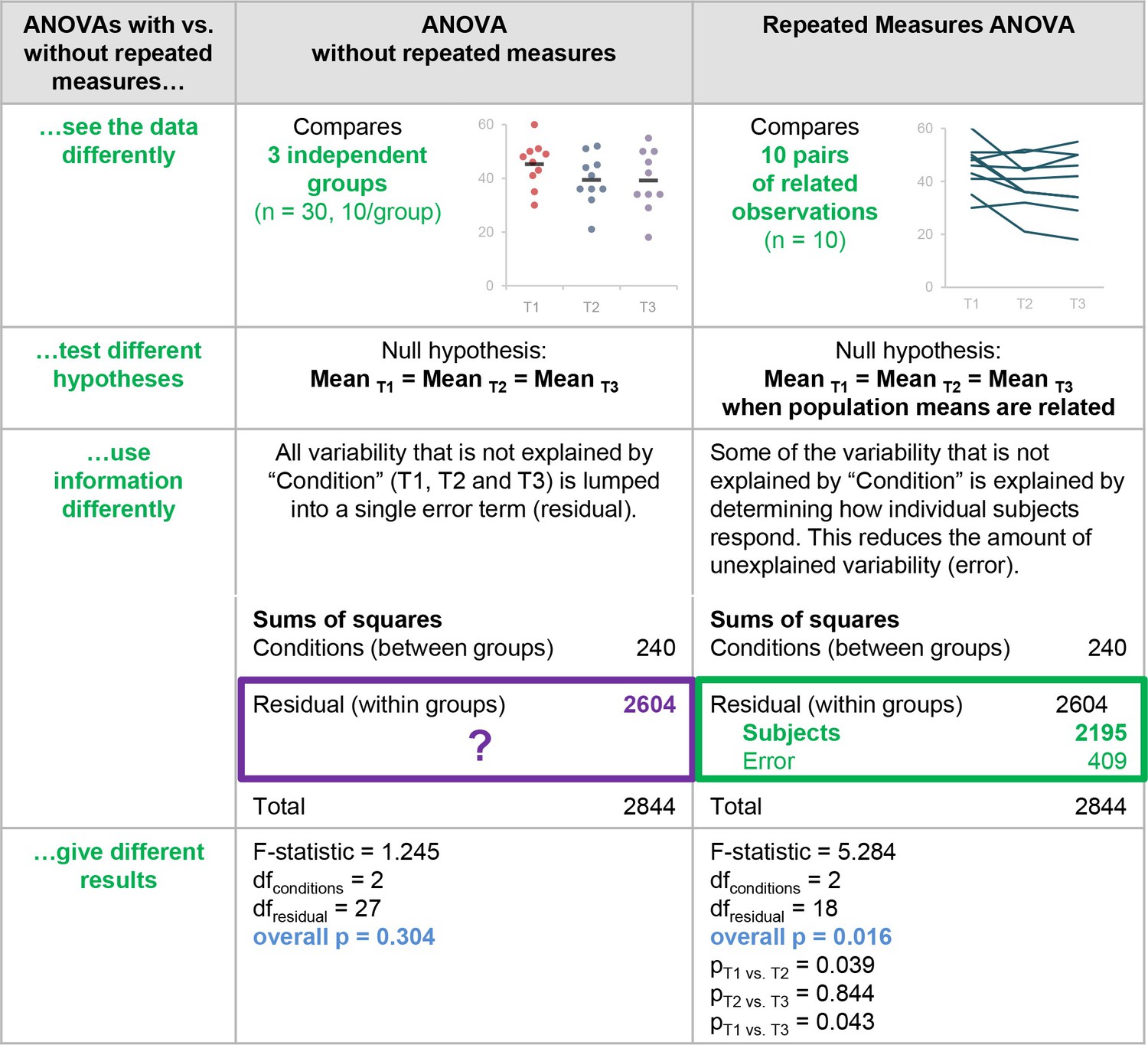
R Correlation
Corrlation
set.seed(0) x <- 1:20 + rnorm(20,sd=5) y <- 1:20 + rnorm(20,sd=5) type <- rep(LETTERS[1:2],each=10) # Make a data frame with the variables dat <- data.frame(x=x, y=y,type=type) |
cor(dat$x,dat$y,method = c("pearson", "kendall", "spearman")[1]) # 0.608 pearson <- function(x, y) var(x, y) / (sd(x) * sd(y)) pearson(dat$x,dat$y) # 0.608063 cor.test(dat$x,dat$y,method="pearson") # Pearson's product-moment correlation # # data: dat$x and dat$y # t = 3.2496, df = 18, p-value = 0.00445 # alternative hypothesis: true correlation is not equal to 0 # 95 percent confidence interval: # 0.2264849 0.8278307 # sample estimates: # cor # 0.608063 cor(dat$x,dat$y,method = c("pearson", "kendall", "spearman")[3]) cor(rank(dat$x),rank(dat$y),method = c("pearson", "kendall", "spearman")[1]) # 0.6015038 ## https://en.wikipedia.org/wiki/Kendall_rank_correlation_coefficient cor(dat$x,dat$y,method = c("pearson", "kendall", "spearman")[2]) cor(rank(dat$x),rank(dat$y),method = c("pearson", "kendall", "spearman")[2]) # 0.4526316 kendall <- function(x,y){ cd = 0 l <- length(x) if (!identical(length(x),length(y))){ stop("Not equal length vectors") } for (i in 1:(l-1)){ for (j in i:l){ cd = cd + sign(x[i] - x[j]) * sign(y[i] - y[j]) }} return((cd/(l*(l-1)/2))) } kendall(dat$x,dat$y) # 0.4526316 |
library(corrplot) corrplot(corr = cor(dat[,-3]), method="number", col="black", cl.pos="n") |
- corrplot(corr, method = c(“circle”, “square”, “ellipse”, “number”, “shade”, “color”, “pie”)(可视化的方法,圆形、方形、椭圆形、数值、阴影、颜色或饼图)
- type = c(“full”, “lower”, “upper”)(展示的方式,可以是完全的、下三角或上三角)
- add = FALSE
- col = NULL(图形展示的颜色,默认以均匀的颜色展示), bg = “white”(背景色), title = “”(标题)
- is.corr = TRUE(FALSE,则为非相关系数的可视化), diag = TRUE(展示对角线上的相关系数)
- outline = FALSE(绘制圆形、方形或椭圆形的轮廓), mar = c(0, 0, 0, 0)(图形的四边间距)
- addgrid.col = NULL(当选择的方法为颜色或阴影时,默认的网格线颜色为白色,否则为灰色)
- addCoef.col = NULL(为相关系数添加颜色,默认不添加相关系数,只有方法为number时,该参数才起作用)
- addCoefasPercent = FALSE(是否将相关系数转换为百分比格式)
- order = c(“original”,“AOE”, “FPC”, “hclust”, “alphabet”)(原始顺序(original)、特征向量角序(AOE)、第一主成分顺序(FPC)、层次聚类顺序(hclust)
- hclust.method = c(“complete”, “ward”,“ward.D”, “ward.D2”, “single”, “average”, “mcquitty”, “median”, “centroid”)(hclust的聚类方法)
- addrect = NULL(hclust的矩形框), rect.col = “black”(矩形框的颜色), rect.lwd = 2(矩形框的线宽)
- tl.pos = NULL(指定文本标签的位置,type=full时,在左边和顶部(lt),type=lower时,在左边和对角线(ld),type=upper时,在顶部和对角线,d表示对角线,n表示不添加文本标签)
- tl.cex = 1(文本标签的大小), tl.col = “red”(文本标签的颜色), tl.offset = 0.4, tl.srt = 90
- cl.pos = NULL(图例(颜色)位置,当type=upper或full时,图例在右表(r),当type=lower时,图例在底部,不需要图例时,只需指定该参数为n)
- cl.lim = NULL, cl.length = NULL, cl.cex = 0.8,cl.ratio = 0.15, cl.align.text = “c”, cl.offset = 0.5
- number.cex = 1, number.font = 2, number.digits = NULL,
addshade = c(“negative”,“positive”, “all”)(若method=shade,则negtive/positive和all,对相关系数加阴影, 正相关系数的阴影是45度,负相关系数的阴影是135度) - shade.lwd = 1(阴影的线宽), shade.col = “white”(阴影线的颜色), p.mat = NULL, sig.level = 0.05
- insig = c(“pch”, “p-value”, “blank”, “n”, “label_sig”),pch = 4, pch.col = “black”, pch.cex = 3
- plotCI = c(“n”, “square”,“circle”, “rect”), lowCI.mat = NULL, uppCI.mat = NULL, na.label = “?”,
na.label.col = “black”, win.asp = 1, …)
pairs(mtcars[,1:7]) |
require(GGally) ggpairs(mtcars[,1:7]) |
library(car) scatterplotMatrix(mtcars[,1:7], diagonal="histogram", smooth=FALSE) |
## Warning in applyDefaults(diagonal, defaults = list(method = ## "adaptiveDensity"), : unnamed diag arguments, will be ignored |
corr <- cor(mtcars[,1:7]) corrplot(corr = corr, method = 'color', order ="AOE", addCoef.col="grey",tl.col = "black",tl.cex = 1,cl.pos = "n") |
corrplot(corr = corr, col = "yellow", order="AOE", outline=FALSE, cl.pos="n",bg="gold") |
corrplot(corr = corr,order="AOE",type="upper",tl.pos="d") corrplot(corr = corr,add=TRUE, type="lower", method="number",order="AOE",diag=F,tl.pos="n", cl.pos="n") |
corrplot(corr = corr, order="hclust", addrect = 3, rect.col = "black",cl.pos = "n",tl.cex = 1.2) |
library(ellipse) colorfun <- colorRamp(c("#4CAF50","white","#F57C00"), space="rgb") plotcorr(corr, col=rgb(colorfun((corr+1)/2), maxColorValue=255),numbers = F, mar = c(0.1, 0.1, 0.1, 0.1)) |
All articles in this blog are licensed under CC BY-NC-SA 4.0 unless stating additionally.
Comment