62. Unique Paths[M]

https://leetcode.com/problems/unique-paths/

Description

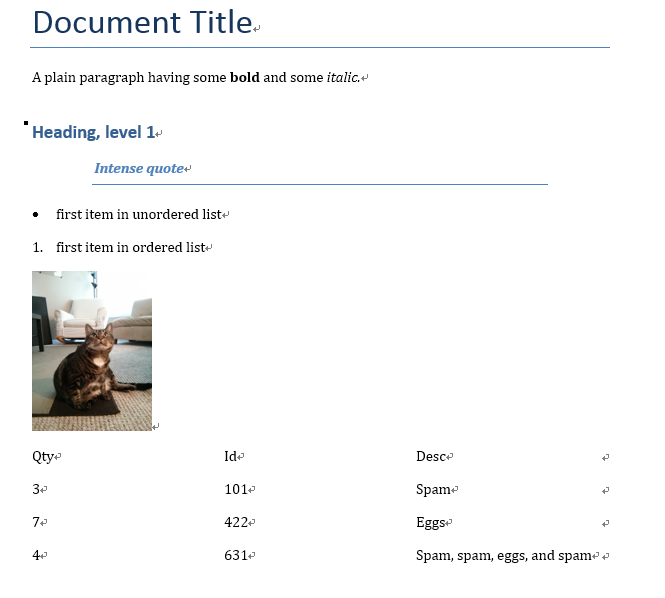
A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

How many possible unique paths are there?

img
Above is a 7 x 3 grid. How many possible unique paths are there?

Example 1:

1
2
3
4
5
6
7
Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right

Example 2:

1
2
Input: m = 7, n = 3
Output: 28

Constraints:

  • 1 <= m, n <= 100
  • It’s guaranteed that the answer will be less than or equal to 2 * 10 ^ 9.

Solution

1

63. Unique Paths II[M]

https://leetcode.com/problems/unique-paths-ii/

Description

A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

Now consider if some obstacles are added to the grids. How many unique paths would there be?

img

An obstacle and empty space is marked as 1 and 0 respectively in the grid.

Note: m and n will be at most 100.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
Input:
[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]
Output: 2
Explanation:
There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right

Solution

1

64. Minimum Path Sum[M]

https://leetcode.com/problems/minimum-path-sum/

Description

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

Example:

1
2
3
4
5
6
7
8
Input:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
Output: 7
Explanation: Because the path 1→3→1→1→1 minimizes the sum.

Solution

1

71. Simplify Path[M]

https://leetcode.com/problems/simplify-path/

Description

Given an absolute path for a file (Unix-style), simplify it. Or in other words, convert it to the canonical path.

In a UNIX-style file system, a period . refers to the current directory. Furthermore, a double period .. moves the directory up a level.

Note that the returned canonical path must always begin with a slash /, and there must be only a single slash / between two directory names. The last directory name (if it exists) must not end with a trailing /. Also, the canonical path must be the shortest string representing the absolute path.

Example 1:

1
2
3
Input: "/home/"
Output: "/home"
Explanation: Note that there is no trailing slash after the last directory name.

Example 2:

1
2
3
Input: "/../"
Output: "/"
Explanation: Going one level up from the root directory is a no-op, as the root level is the highest level you can go.

Example 3:

1
2
3
Input: "/home//foo/"
Output: "/home/foo"
Explanation: In the canonical path, multiple consecutive slashes are replaced by a single one.

Example 4:

1
2
Input: "/a/./b/../../c/"
Output: "/c"

Example 5:

1
2
Input: "/a/../../b/../c//.//"
Output: "/c"

Example 6:

1
2
Input: "/a//b////c/d//././/.."
Output: "/a/b/c"

Solution

1

388. Longest Absolute File Path[M]

https://leetcode.com/problems/longest-absolute-file-path/

Description

Suppose we abstract our file system by a string in the following manner:

The string "dir\n\tsubdir1\n\tsubdir2\n\t\tfile.ext" represents:

1
2
3
4
dir
    subdir1
    subdir2
        file.ext

The directory dir contains an empty sub-directory subdir1 and a sub-directory subdir2 containing a file file.ext.

The string "dir\n\tsubdir1\n\t\tfile1.ext\n\t\tsubsubdir1\n\tsubdir2\n\t\tsubsubdir2\n\t\t\tfile2.ext" represents:

1
2
3
4
5
6
7
dir
    subdir1
        file1.ext
        subsubdir1
    subdir2
        subsubdir2
            file2.ext

The directory dir contains two sub-directories subdir1 and subdir2. subdir1 contains a file file1.ext and an empty second-level sub-directory subsubdir1. subdir2 contains a second-level sub-directory subsubdir2 containing a file file2.ext.

We are interested in finding the longest (number of characters) absolute path to a file within our file system. For example, in the second example above, the longest absolute path is "dir/subdir2/subsubdir2/file2.ext", and its length is 32 (not including the double quotes).

Given a string representing the file system in the above format, return the length of the longest absolute path to file in the abstracted file system. If there is no file in the system, return 0.

Note:

  • The name of a file contains at least a . and an extension.
  • The name of a directory or sub-directory will not contain a ..

Time complexity required: O(n) where n is the size of the input string.

Notice that a/aa/aaa/file1.txt is not the longest file path, if there is another path aaaaaaaaaaaaaaaaaaaaa/sth.png.

Solution

1