Traversal

94. Binary Tree Inorder Traversal[M]

https://leetcode.com/problems/binary-tree-inorder-traversal/

Description

Given a binary tree, return the inorder traversal of its nodes’ values.

Example:

1
2
3
4
5
6
7
8
Input: [1,null,2,3]
   1
    \
     2
    /
   3

Output: [1,3,2]

Follow up: Recursive solution is trivial, could you do it iteratively?

Solution

https://leetcode.com/problems/binary-tree-inorder-traversal/solution/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        if root is None:
            return []
        res = []
        stack = [root]
        while len(stack) > 0:
            curr = stack.pop()
            if not isinstance(curr, TreeNode):
                res.append(curr)
                continue
            if curr.right is not None:
                stack.append(curr.right)
            stack.append(curr.val)
            if curr.left is not None:
                stack.append(curr.left)
        return res

145. Binary Tree Postorder Traversals[H]

https://leetcode.com/problems/binary-tree-postorder-traversal/

Description

Given a binary tree, return the postorder traversal of its nodes’ values.

Example:

1
2
3
4
5
6
7
8
Input: [1,null,2,3]
   1
    \
     2
    /
   3

Output: [3,2,1]

Follow up: Recursive solution is trivial, could you do it iteratively?

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def postorderTraversal(self, root: TreeNode) -> List[int]:
        if root is None:
            return []
        res = []; stack = [root]
        while len(stack) > 0:
            curr = stack.pop()
            if not isinstance(curr, TreeNode):
                res.append(curr)
                continue
            stack.append(curr.val)
            if curr.right is not None:
                stack.append(curr.right)
            if curr.left is not None:
                stack.append(curr.left)
        return res

144. Binary Tree Preorder Traversal[M]

https://leetcode.com/problems/binary-tree-preorder-traversal/

Description

Given a binary tree, return the preorder traversal of its nodes’ values.

Example:

1
2
3
4
5
6
7
8
Input: [1,null,2,3]
   1
    \
     2
    /
   3

Output: [1,2,3]

Follow up: Recursive solution is trivial, could you do it iteratively?

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        # stack
        if root is None:
            return []
        res = []
        stack = [root]
        while len(stack) > 0:
            curr = stack.pop()
            res.append(curr.val)
            if curr.right is not None:
                stack.append(curr.right)
            if curr.left is not None:
                stack.append(curr.left)
        return res

102. Binary Tree Level Order Traversal[M]

https://leetcode.com/problems/binary-tree-level-order-traversal/

Description

Given a binary tree, return the level order traversal of its nodes’ values. (ie, from left to right, level by level).

For example:
Given binary tree [3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

return its level order traversal as:

1
2
3
4
5
[
  [3],
  [9,20],
  [15,7]
]

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        # https://leetcode.com/discuss/90680/9-lines-python-code
        if root is None:
            return []
        q = [[root]]
        for level in q:
            record = []
            for node in level:
                if node.left:
                    record.append(node.left)
                if node.right:
                    record.append(node.right)
            if record:
                q.append(record)
        return [[x.val for x in level] for level in q]

103. Binary Tree Zigzag Level Order Traversal[M]

https://leetcode.com/problems/binary-tree-zigzag-level-order-traversal/

Description

Given a binary tree, return the zigzag level order traversal of its nodes’ values. (ie, from left to right, then right to left for the next level and alternate between).

For example:
Given binary tree [3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

return its zigzag level order traversal as:

1
2
3
4
5
[
  [3],
  [20,9],
  [15,7]
]

Solution

1

105. Construct Binary Tree from Preorder and Inorder Traversal[M]

https://leetcode.com/problems/divide-two-integers/

Description

Given preorder and inorder traversal of a tree, construct the binary tree.

Note:
You may assume that duplicates do not exist in the tree.

For example, given

1
2
preorder = [3,9,20,15,7]
inorder = [9,3,15,20,7]

Return the following binary tree:

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

Solution

106. Construct Binary Tree from Inorder and Postorder Traversal[M]

https://leetcode.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/

Description

Given inorder and postorder traversal of a tree, construct the binary tree.

Note:
You may assume that duplicates do not exist in the tree.

For example, given

1
2
inorder = [9,3,15,20,7]
postorder = [9,15,7,20,3]

Return the following binary tree:

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

Solution

107. Binary Tree Level Order Traversal II[E]

https://leetcode.com/problems/binary-tree-level-order-traversal-ii/

Description

Given a binary tree, return the bottom-up level order traversal of its nodes’ values. (ie, from left to right, level by level from leaf to root).

For example:
Given binary tree [3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

return its bottom-up level order traversal as:

1
2
3
4
5
[
  [15,7],
  [9,20],
  [3]
]

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def levelOrderBottom(self, root: TreeNode) -> List[List[int]]:
        if root is None:
            return []
        # use stack
        stack = [[root]]
        res = []
        while len(stack) > 0:
            top = stack.pop()
            res.insert(0, [t.val for t in top])
            temp = []
            for node in top:
                if node.left is not None:
                    temp.append(node.left)
                if node.right is not None:
                    temp.append(node.right)
            if len(temp) > 0:
                stack.append(temp)
        return res

Unique

95. Unique Binary Search Trees II[M]

https://leetcode.com/problems/unique-binary-search-trees-ii/

Description

iven an integer n, generate all structurally unique BST’s (binary search trees) that store values 1 … n.

Example:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Input: 3
Output:
[
  [1,null,3,2],
  [3,2,null,1],
  [3,1,null,null,2],
  [2,1,3],
  [1,null,2,null,3]
]
Explanation:
The above output corresponds to the 5 unique BST's shown below:

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

Constraints:

  • 0 <= n <= 8

Solution

96. Unique Binary Search Trees[M]

https://leetcode.com/problems/unique-binary-search-trees/

Description

Given n, how many structurally unique BST’s (binary search trees) that store values 1 … n?

Example:

1
2
3
4
5
6
7
8
9
10
Input: 3
Output: 5
Explanation:
Given n = 3, there are a total of 5 unique BST's:

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

Constraints:

  • 1 <= n <= 19

Solution

https://leetcode.com/discuss/86650/fantastic-clean-java-dp-solution-with-detail-explaination

1
2
3
4
5
6
7
8
9
class Solution:
    def numTrees(self, n: int) -> int:
        dp = [0] * (n + 1)
        dp[0] = 1
        dp[1] = 1
        for level in range(2, n + 1):
            for root in range(1, level + 1):
                dp[level] += dp[level - root] * dp[root - 1]
        return dp[n]

99. Recover Binary Search Tree[H]

https://leetcode.com/problems/recover-binary-search-tree/

Description

Two elements of a binary search tree (BST) are swapped by mistake.

Recover the tree without changing its structure.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Input: [1,3,null,null,2]

   1
  /
 3
  \
   2

Output: [3,1,null,null,2]

   3
  /
 1
  \
   2

Example 2:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Input: [3,1,4,null,null,2]

  3
 / \
1   4
   /
  2

Output: [2,1,4,null,null,3]

  2
 / \
1   4
   /
  3

Follow up:

  • A solution using O(n) space is pretty straight forward.
  • Could you devise a constant space solution?

Solution

1

98. Validate Binary Search Tree[M]

https://leetcode.com/problems/validate-binary-search-tree/

Description

Given a binary tree, determine if it is a valid binary search tree (BST).

Assume a BST is defined as follows:

  • The left subtree of a node contains only nodes with keys less than the node’s key.
  • The right subtree of a node contains only nodes with keys greater than the node’s key.
  • Both the left and right subtrees must also be binary search trees.

Example 1:

1
2
3
4
5
6
    2
   / \
  1   3

Input: [2,1,3]
Output: true

Example 2:

1
2
3
4
5
6
7
8
9
    5
   / \
  1   4
     / \
    3   6

Input: [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.

Solution

100. Same Tree[E]

https://leetcode.com/problems/same-tree/

Description

Given two binary trees, write a function to check if they are the same or not.

Two binary trees are considered the same if they are structurally identical and the nodes have the same value.

Example 1:

1
2
3
4
5
6
7
Input:     1         1
          / \       / \
         2   3     2   3

        [1,2,3],   [1,2,3]

Output: true

Example 2:

1
2
3
4
5
6
7
Input:     1         1
          /           \
         2             2

        [1,2],     [1,null,2]

Output: false

Example 3:

1
2
3
4
5
Input:     1         1
          / \       / \
         2   1     1   2

        [1,2,1],   [1,1,2]

Solution

https://leetcode.com/problems/same-tree/solution/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
        if p == None and q == None: 
            return True
        elif p != None and q != None:
            if p.val != q.val: return False
        else:
            return False
        if not self.isSameTree(p.left, q.left): return False
        return  self.isSameTree(p.right, q.right)           
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {boolean}
 */
var isSameTree = function(p, q) {
    return JSON.stringify(p) === JSON.stringify(q)
};

Depth

104. Maximum Depth of Binary Tree[E]

https://leetcode.com/problems/maximum-depth-of-binary-tree/

Description

Given a binary tree, find its maximum depth.

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Note: A leaf is a node with no children.

Example:

Given binary tree [3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

return its depth = 3.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: TreeNode) -> int:
         if root is None:
            return 0
        ld = self.maxDepth(root.left)
        rd = self.maxDepth(root.right)
        return 1 + max(ld, rd)

111. Minimum Depth of Binary Tree[E]

https://leetcode.com/problems/minimum-depth-of-binary-tree/

Description

ven a binary tree, find its minimum depth.

The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.

Note: A leaf is a node with no children.

Example:

Given binary tree [3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

Solution

Convert

108. Convert Sorted Array to Binary Search Tree[E]

https://leetcode.com/problems/convert-sorted-array-to-binary-search-tree/

Description

ven an array where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example:

1
2
3
4
5
6
7
8
9
Given the sorted array: [-10,-3,0,5,9],

One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:

      0
     / \
   -3   9
   /   /
 -10  5

Solution

109. Convert Sorted List to Binary Search Tree[M]

https://leetcode.com/problems/convert-sorted-list-to-binary-search-tree/

Description

Given a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example:

1
2
3
4
5
6
7
8
9
Given the sorted linked list: [-10,-3,0,5,9],

One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:

      0
     / \
   -3   9
   /   /
 -10  5

Solution

1

114. Flatten Binary Tree to Linked List[M]

https://leetcode.com/problems/flatten-binary-tree-to-linked-list/

Description

Given a binary tree, flatten it to a linked list in-place.

For example, given the following tree:

1
2
3
4
5
    1
   / \
  2   5
 / \   \
3   4   6

The flattened tree should look like:

1
2
3
4
5
6
7
8
9
10
11
1
 \
  2
   \
    3
     \
      4
       \
        5
         \
          6

Solution

1

110. Balanced Binary Tree[E]

https://leetcode.com/problems/balanced-binary-tree/

Description

Given a binary tree, determine if it is height-balanced.

For this problem, a height-balanced binary tree is defined as:

a binary tree in which the left and right subtrees of every node differ in height by no more than 1.

Example 1:

Given the following tree [3,9,20,null,null,15,7]:

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

Return true.

Example 2:

Given the following tree [1,2,2,3,3,null,null,4,4]:

1
2
3
4
5
6
7
      1
     / \
    2   2
   / \
  3   3
 / \
4   4

Return false.

Solution

124. Binary Tree Maximum Path Sum[H]

https://leetcode.com/problems/binary-tree-maximum-path-sum/

Description

Given a non-empty binary tree, find the maximum path sum.

For this problem, a path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.

Example 1:

1
2
3
4
5
6
7
Input: [1,2,3]

       1
      / \
     2   3

Output: 6

Example 2:

1
2
3
4
5
6
7
8
9
Input: [-10,9,20,null,null,15,7]

   -10
   / \
  9  20
    /  \
   15   7

Output: 42

Solution

226. Invert Binary Tree[E]

https://leetcode.com/problems/invert-binary-tree/

Description

Invert a binary tree.

Example:

Input:

1
2
3
4
5
     4
   /   \
  2     7
 / \   / \
1   3 6   9

Output:

1
2
3
4
5
     4
   /   \
  7     2
 / \   / \
9   6 3   1

Trivia:
This problem was inspired by this original tweet by Max Howell:

Google: 90% of our engineers use the software you wrote (Homebrew), but you can’t invert a binary tree on a whiteboard so f*** off.

Solution

1

235. Lowest Common Ancestor of a Binary Search Tree[E]

https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree/

Description

Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Given binary search tree: root = [6,2,8,0,4,7,9,null,null,3,5]

img

Example 1:

1
2
3
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

Example 2:

1
2
3
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Constraints:

  • All of the nodes’ values will be unique.
  • p and q are different and both values will exist in the BST.

Solution

https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree/solution/

236. Lowest Common Ancestor of a Binary Tree[M]

https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-tree/

Description

Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Given the following binary tree: root = [3,5,1,6,2,0,8,null,null,7,4]

img

Example 1:

1
2
3
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.

Example 2:

1
2
3
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.

Note:

  • All of the nodes’ values will be unique.
  • p and q are different and both values will exist in the binary tree.

Solution

257. Binary Tree Paths[E]

https://leetcode.com/problems/binary-tree-paths/

Description

Given a binary tree, return all root-to-leaf paths.

Note: A leaf is a node with no children.

Example:

1
2
3
4
5
6
7
8
9
10
11
Input:

   1
 /   \
2     3
 \
  5

Output: ["1->2->5", "1->3"]

Explanation: All root-to-leaf paths are: 1->2->5, 1->3

Solution

543. Diameter of Binary Tree[E]

https://leetcode.com/problems/diameter-of-binary-tree/

Description

Given a binary tree, you need to compute the length of the diameter of the tree. The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.

Example:
Given a binary tree

1
2
3
4
5
    1
   / \
  2   3
 / \     
4   5

Return 3, which is the length of the path [4,2,1,3] or [5,2,1,3].

Note: The length of path between two nodes is represented by the number of edges between them.

Solution

https://leetcode.com/problems/diameter-of-binary-tree/solution/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def diameterOfBinaryTree(self, root: TreeNode) -> int:
        self.ans = 1
        def depth(node):
            if not node: return 0
            L = depth(node.left)
            R = depth(node.right)
            self.ans = max(self.ans, L+R+1)
            return max(L, R) + 1

        depth(root)
        # number of nodes - 1 = length
        return self.ans - 1

617. Merge Two Binary Trees[E]

https://leetcode.com/problems/merge-two-binary-trees/

Description

Given two binary trees and imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not.

You need to merge them into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of new tree.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Input: 
	Tree 1                     Tree 2                  
          1                         2                             
         / \                       / \                            
        3   2                     1   3                        
       /                           \   \                      
      5                             4   7                  
Output: 
Merged tree:
	     3
	    / \
	   4   5
	  / \   \ 
	 5   4   7

Note: The merging process must start from the root nodes of both trees.

Solution

https://leetcode.com/problems/merge-two-binary-trees/solution/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def mergeTrees(self, t1: TreeNode, t2: TreeNode) -> TreeNode:
        if t1 is None:
            return t2
        if t2 is None:
            return t1
        t1.val += t2.val
        t1.left = self.mergeTrees(t1.left, t2.left)
        t1.right = self.mergeTrees(t1.right, t2.right)
        return t1

654. Maximum Binary Tree[M]

https://leetcode.com/problems/maximum-binary-tree/

Description

Given an integer array with no duplicates. A maximum tree building on this array is defined as follow:

  1. The root is the maximum number in the array.
  2. The left subtree is the maximum tree constructed from left part subarray divided by the maximum number.
  3. The right subtree is the maximum tree constructed from right part subarray divided by the maximum number.

Construct the maximum tree by the given array and output the root node of this tree.

Example 1:

1
2
3
4
5
6
7
8
9
10
Input: [3,2,1,6,0,5]
Output: return the tree root node representing the following tree:

      6
    /   \
   3     5
    \    / 
     2  0   
       \
        1

Note:

  1. The size of the given array will be in the range [1,1000].

Solution

https://leetcode.com/problems/maximum-binary-tree/solution/

671. Second Minimum Node In a Binary Tree[E]

https://leetcode.com/problems/divide-two-integers/

Description

Given a non-empty special binary tree consisting of nodes with the non-negative value, where each node in this tree has exactly two or zero sub-node. If the node has two sub-nodes, then this node’s value is the smaller value among its two sub-nodes. More formally, the property root.val = min(root.left.val, root.right.val) always holds.

Given such a binary tree, you need to output the second minimum value in the set made of all the nodes’ value in the whole tree.

If no such second minimum value exists, output -1 instead.

Example 1:

1
2
3
4
5
6
7
8
9
Input: 
    2
   / \
  2   5
     / \
    5   7

Output: 5
Explanation: The smallest value is 2, the second smallest value is 5.

Example 2:

1
2
3
4
5
6
7
Input: 
    2
   / \
  2   2

Output: -1
Explanation: The smallest value is 2, but there isn't any second smallest value.

Solution

https://leetcode.com/problems/second-minimum-node-in-a-binary-tree/solution/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def findSecondMinimumValue(self, root: TreeNode) -> int:
        if not root:
            return -1
        ans = float('inf')
        min_val = root.val
        stack = [root]
        while stack:
            curr = stack.pop()
            if not curr:
                continue
            if min_val < curr.val < ans:
                ans = curr.val
            elif curr.val == min_val:
                stack.append(curr.left)
                stack.append(curr.right)
        return ans if ans < float('inf') else -1

700. Search in a Binary Search Tree[E]

https://leetcode.com/problems/search-in-a-binary-search-tree/

Description

Given the root node of a binary search tree (BST) and a value. You need to find the node in the BST that the node’s value equals the given value. Return the subtree rooted with that node. If such node doesn’t exist, you should return NULL.

For example,

1
2
3
4
5
6
7
8
Given the tree:
        4
       / \
      2   7
     / \
    1   3

And the value to search: 2

You should return this subtree:

1
2
3
  2     
 / \   
1   3

In the example above, if we want to search the value 5, since there is no node with value 5, we should return NULL.

Note that an empty tree is represented by NULL, therefore you would see the expected output (serialized tree format) as [], not null.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def searchBST(self, root: TreeNode, val: int) -> TreeNode:
        while root:
            if root.val == val:
                return root
            elif root.val > val:
                root = root.left
            else:
                root = root.right
        return root

101. Symmetric Tree[E]

https://leetcode.com/problems/symmetric-tree/

Description

Share

Given a binary tree, check whether it is a mirror of itself (ie, symmetric around its center).

For example, this binary tree [1,2,2,3,4,4,3] is symmetric:

1
2
3
4
5
    1
   / \
  2   2
 / \ / \
3  4 4  3

But the following [1,2,2,null,3,null,3] is not:

1
2
3
4
5
  1
 / \
2   2
 \   \
 3    3

Follow up: Solve it both recursively and iteratively.

Solution

208. Implement Trie (Prefix Tree)[M]

https://leetcode.com/problems/implement-trie-prefix-tree//

Description

Implement a trie with insert, search, and startsWith methods.

Example:

1
2
3
4
5
6
7
8
Trie trie = new Trie();

trie.insert("apple");
trie.search("apple");   // returns true
trie.search("app");     // returns false
trie.startsWith("app"); // returns true
trie.insert("app");   
trie.search("app");     // returns true

Note:

  • You may assume that all inputs are consist of lowercase letters a-z.
  • All inputs are guaranteed to be non-empty strings.

Solution

538. Convert BST to Greater Tree[E]

https://leetcode.com/problems/convert-bst-to-greater-tree/

Description

Given a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus sum of all keys greater than the original key in BST.

Example:

1
2
3
4
5
6
7
8
9
Input: The root of a Binary Search Tree like this:
              5
            /   \
           2     13

Output: The root of a Greater Tree like this:
             18
            /   \
          20     13

Note: This question is the same as 1038: https://leetcode.com/problems/binary-search-tree-to-greater-sum-tree/

Solution

572. Subtree of Another Tree[E]

https://leetcode.com/problems/subtree-of-another-tree/

Description

Given two non-empty binary trees s and t, check whether tree t has exactly the same structure and node values with a subtree of s. A subtree of s is a tree consists of a node in s and all of this node’s descendants. The tree s could also be considered as a subtree of itself.

Example 1:
Given tree s:

1
2
3
4
5
    3
   / \
  4   5
 / \
1   2

Given tree t:

1
2
3
  4 
 / \
1   2

Return true, because t has the same structure and node values with a subtree of s.

Example 2:
Given tree s:

1
2
3
4
5
6
7
    3
   / \
  4   5
 / \
1   2
   /
  0

Given tree t:

1
2
3
  4
 / \
1   2

Return false.

Solution

872. Leaf-Similar Trees[E]

https://leetcode.com/problems/leaf-similar-trees/

Description

Consider all the leaves of a binary tree. From left to right order, the values of those leaves form a leaf value sequence.

img

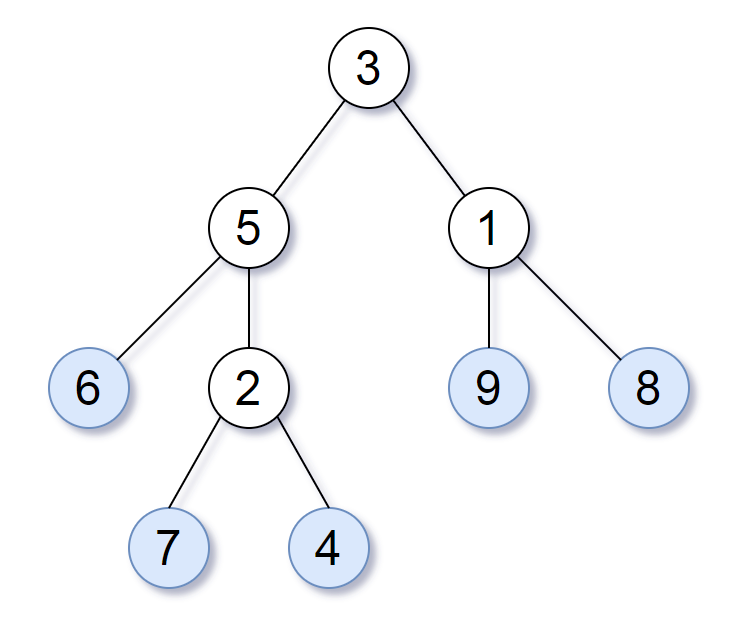
For example, in the given tree above, the leaf value sequence is (6, 7, 4, 9, 8).

Two binary trees are considered leaf-similar if their leaf value sequence is the same.

Return true if and only if the two given trees with head nodes root1 and root2 are leaf-similar.

Constraints:

  • Both of the given trees will have between 1 and 200 nodes.
  • Both of the given trees will have values between 0 and 200

Solution

116. Populating Next Right Pointers in Each Node[M]

https://leetcode.com/problems/populating-next-right-pointers-in-each-node/

Description

You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:

1
2
3
4
5
6
struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Follow up:

  • You may only use constant extra space.
  • Recursive approach is fine, you may assume implicit stack space does not count as extra space for this problem.

Example 1:

img

1
2
3
Input: root = [1,2,3,4,5,6,7]
Output: [1,#,2,3,#,4,5,6,7,#]
Explanation: Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.

Constraints:

  • The number of nodes in the given tree is less than 4096.
  • -1000 <= node.val <= 1000

Solution

1

117. Populating Next Right Pointers in Each Node II[M]

https://leetcode.com/problems/populating-next-right-pointers-in-each-node-ii/

Description

Given a binary tree

1
2
3
4
5
6
struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Follow up:

  • You may only use constant extra space.
  • Recursive approach is fine, you may assume implicit stack space does not count as extra space for this problem.

Example 1:

img

1
2
3
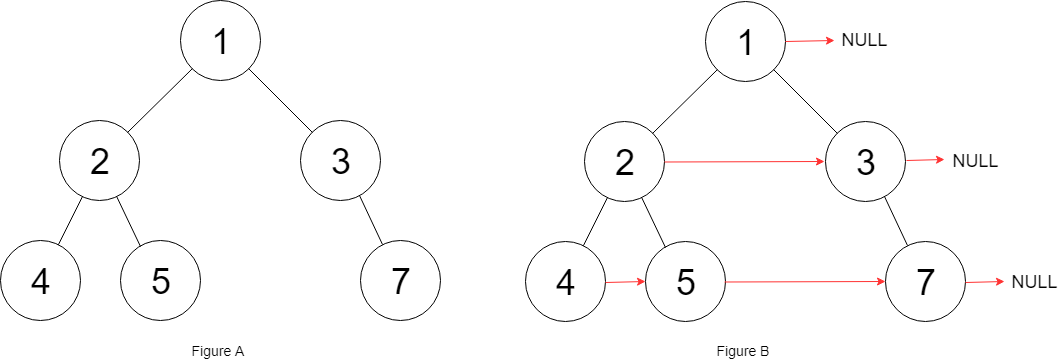
Input: root = [1,2,3,4,5,null,7]
Output: [1,#,2,3,#,4,5,7,#]
Explanation: Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.

Constraints:

  • The number of nodes in the given tree is less than 6000.
  • -100 <= node.val <= 100

Solution

1