排序算法可以分为内部排序和外部排序。

内部排序是在内存数据记录中进行排序。

外部排序需要访问外存，因排序的数据很大，一次不能容纳全部的排序记录。

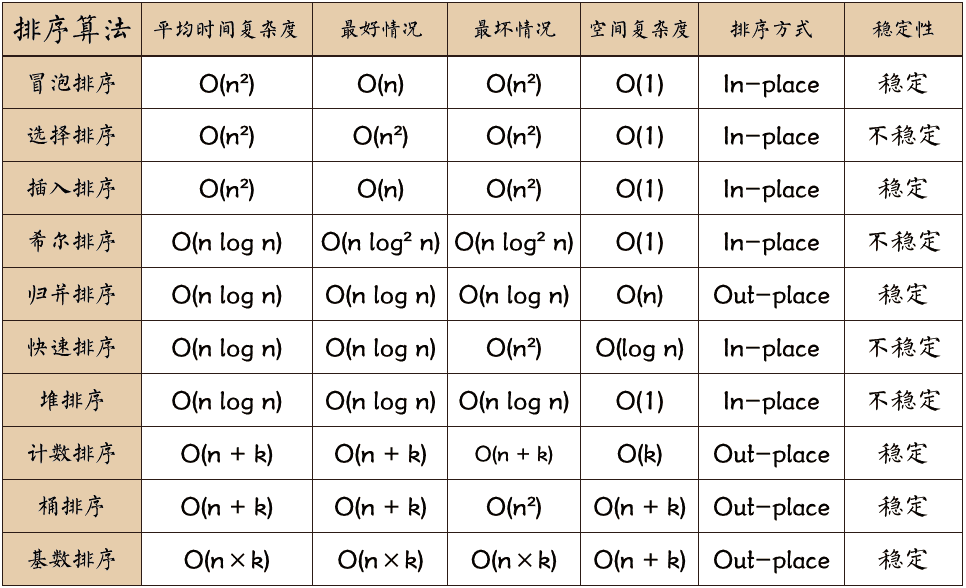
常见的内部排序算法有用一张图概括如下：

sort_algorithm_complexity

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
"""
排序 - 冒泡排序、选择排序、归并排序、快速排序
冒泡排序 - O(n ** 2)：两两比较，大的下沉
35, 97, 12, 68, 55, 73, 81, 40
35, 12, 68, 55, 73, 81, 40, [97]
12, 35, 55, 68, 73, 40, [81]
12, 35, 55, 68, 40, [73]
...
选择排序 - O(n ** 2)：每次从剩下元素中选择最小
-----------------------------------------
归并排序 - O(n * log_2 n) - 高级排序算法
35, 97, 12, 68, 55, 73, 81, 40
[35, 97, 12, 68], [55, 73, 81, 40]
[35, 97], [12, 68], [55, 73], [81, 40]
[35], [97], [12], [68], [55], [73], [81], [40]
[35, 97], [12, 68], [55, 73], [40, 81]
[12, 35, 68, 97], [40, 55, 73, 81]
[12, 35, 40, 55, 68, 73, 81, 97]
-----------------------------------------
快速排序 - 以枢轴为界将列表中的元素划分为两个部分，左边都比枢轴小，右边都比枢轴大
35, 97, 12, 68, 55, 73, 81, 40
35, 12, [40], 68, 55, 73, 81, 97
[12], 35, [40], 68, 55, 73, 81, [97]
[12], 35, [40], 55, [68], 73, 81, [97]
[12], 35, [40], 55, [68], 73, [81], [97]
"""





def select_sort(origin_items, comp=lambda x, y: x < y):
    """简单选择排序"""
    items = origin_items[:]
    for i in range(len(items) - 1):
        min_index = i
        for j in range(i + 1, len(items)):
            if comp(items[j], items[min_index]):
                min_index = j
        items[i], items[min_index] = items[min_index], items[i]
    return items


# 函数的设计要尽量做到无副作用（不影响调用者）
# 9 1 2 3 4 5 6 7 8
# 9 2 3 4 5 6 7 8 1
# *前面的参数叫位置参数，传参时只需要对号入座即可
# *后面的参数叫命名关键字参数，传参时必须给出参数名和参数值
# *args - 可变参数 - 元组
# **kwargs - 关键字参数 - 字典
def bubble_sort(origin_items, *, comp=lambda x, y: x > y):
    """冒泡排序"""
    items = origin_items[:]
    for i in range(1, len(items)):
        swapped = False
        for j in range(i - 1, len(items) - i):
            if comp(items[j], items[j + 1]):
                items[j], items[j + 1] = items[j + 1], items[j]
                swapped = True
        if swapped:
            swapped = False
            for j in range(len(items) - i - 1, i - 1, -1):
                if comp(items[j - 1], items[j]):
                    items[j], items[j - 1] = items[j - 1], items[j]
                    swapped = True
        if not swapped:
            break
    return items


def merge_sort(items, comp=lambda x, y: x <= y):
    """归并排序"""
    if len(items) < 2:
        return items[:]
    mid = len(items) // 2
    left = merge_sort(items[:mid], comp)
    right = merge_sort(items[mid:], comp)
    return merge(left, right, comp)


def merge(items1, items2, comp=lambda x, y: x <= y):
    """合并（将两个有序列表合并成一个新的有序列表）"""
    items = []
    index1, index2 = 0, 0
    while index1 < len(items1) and index2 < len(items2):
        if comp(items1[index1], items2[index2]):
            items.append(items1[index1])
            index1 += 1
        else:
            items.append(items2[index2])
            index2 += 1
    items += items1[index1:]
    items += items2[index2:]
    return items


def quick_sort(origin_items, comp=lambda x, y: x <= y):
    """快速排序"""
    items = origin_items[:]
    _quick_sort(items, 0, len(items) - 1, comp)
    return items


def _quick_sort(items, start, end, comp):
    """递归调用划分和排序"""
    if start < end:
        pos = _partition(items, start, end, comp)
        _quick_sort(items, start, pos - 1, comp)
        _quick_sort(items, pos + 1, end, comp)


def _partition(items, start, end, comp):
    """划分"""
    pivot = items[end]
    i = start - 1
    for j in range(start, end):
        if comp(items[j], pivot):
            i += 1
            items[i], items[j] = items[j], items[i]
    items[i + 1], items[end] = items[end], items[i + 1]
    return i + 1


def main():
    """主函数"""
    items = [35, 97, 12, 68, 55, 73, 81, 40]
    # print(bubble_sort(items))
    # print(select_sort(items))
    # print(merge_sort(items))
    print(quick_sort(items))
    items2 = [
        Person('Wang', 25), Person('Luo', 39),
        Person('Zhang', 50), Person('He', 20)
    ]
    # print(bubble_sort(items2, comp=lambda p1, p2: p1.age > p2.age))
    # print(select_sort(items2, comp=lambda p1, p2: p1.name < p2.name))
    # print(merge_sort(items2, comp=lambda p1, p2: p1.age <= p2.age))
    print(quick_sort(items2, comp=lambda p1, p2: p1.age <= p2.age))
    items3 = ['apple', 'orange', 'watermelon', 'durian', 'pear']
    # print(bubble_sort(items3))
    # print(bubble_sort(items3, comp=lambda x, y: len(x) > len(y)))
    # print(merge_sort(items3))
    print(merge_sort(items3))


if __name__ == '__main__':
    main()

热身

设计一个函数返回传入的列表中最大和第二大以及最小和第二小的元素的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def maxmin2(x):
    m1, m2 = (x[0], x[1]) if x[0] > x[1] else (x[1], x[0])
    m3, m4 = m2, m1
    for idx in range(2, len(x)):
        if x[idx] > m1:
            m2 = m1
            m1 = x[idx]
        elif x[idx] > m2:
            m2 = x[idx]
        if x[idx] < m3:
            m4 = m3
            m3 = x[index] 
        elif x[idx] < m4:
            m4 = x[idx] 
    return m1, m2, m3, m4
maxmin2(array)

冒泡排序(Bubble sort)

我们先看一个简单的例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
array = [1, 2, 5, 3, 6, 8, 4]
## len(array) - 1:取数组的长度减一,不然j+1必然会list idx out of range
# [.<<<<<<<<] [>.......]
for i in range((len(array) - 1), 0, -1):
    ## 需要重复数组的长度减一次，每次最后一个数字必然是最大的
    for j in range(0, i):
        ## 比较相邻的元素。如果第一个比第二个大，就交换
        if array[j] > array[j + 1]:
            ## Python就不用temp临时空杯子了
            array[j], array[j + 1] = array[j + 1], array[j]
print(array)

## 也可以换个循环方式，实质是一样的

for i in range(len(array)):
    for j in range(len(array)-i-1):
        # print(i,j)
        if array[j] > array[j + 1]:
            array[j], array[j + 1] = array[j + 1], array[j]

我们再使用swapped变量优化一下以上算法，判断当前数组是否已排序，减少多余的循环。同时传入comp参数进行排序选择。

1
2
3
4
5
6
7
8
9
10
11
12
13
def bubble_sort(items, comp=lambda x, y: x > y):
    for i in range(len(items) - 1):
        swapped = False
        for j in range(len(items) - 1 - i):
            if comp(items[j], items[j + 1]):
                items[j], items[j + 1] = items[j + 1], items[j]
                swapped = True
        if not swapped:
            break
    return items

bubble_sort(array,comp=lambda x, y: x < y)
# [17, 12, 8, 6, 6, 5, 4, 3, 2, 1]

这里我们换一个思路，通过传入一个*numbers可变参数，通过比较num[j] 和 num[i]进行冒泡排序：

1
2
3
4
5
6
7
8
9
10
11
def bubble_sort2(*numbers):
    num = list(numbers)
    for i in range(1, len(num)):
        idx = ["< " + str(num[i] ) + "?"]
        print(str(num[:i] + idx))
        for j in range(i):
            if num[j] > num[i]:
                num[j], num[i] = num[i], num[j]
                print(num)
    return num
bubble_sort2(3, 1, 5, 7, 5, 8, 4)
1
2
3
4
5
6
7
8
9
10
11
[3, '< 1?']
[1, 3, 5, 7, 5, 8, 4]
[1, 3, '< 5?']
[1, 3, 5, '< 7?']
[1, 3, 5, 7, '< 5?']
[1, 3, 5, 5, 7, 8, 4]
[1, 3, 5, 5, 7, '< 8?']
[1, 3, 5, 5, 7, 8, '< 4?']
[1, 3, 4, 5, 7, 8, 5]
[1, 3, 4, 5, 5, 8, 7]
[1, 3, 4, 5, 5, 7, 8]

双向冒泡排序（也称鸡尾酒排序、搅拌排序）

双向冒泡排序，在完成一次从左往右的冒泡排序后，再从右往左进行冒泡，从而把小的元素放在左边。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def bubble_sort(items, comp=lambda x, y: x > y):
    for i in range(len(items) - 1):
        swapped = False
        for j in range(i, len(items) - 1 - i):  # 正向：把当前循环最大的放到最后
            if comp(items[j], items[j + 1]):
                items[j], items[j + 1] = items[j + 1], items[j]
                swapped = True
        if swapped:
            swapped = False
            for j in range(len(items) - 2 - i, i, -1):  # 反向：把当前循环最小的放到最前
                if comp(items[j - 1], items[j]):
                    items[j], items[j - 1] = items[j - 1], items[j]
                    swapped = True
        if not swapped:
            break
    return items

快速排序

  • 从数列中挑出一个元素，称为 “基准”（pivot）;
  • 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
  • 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
def partition(arr,low,high): 
    i = ( low-1 )         # 最小元素索引
    pivot = arr[high]     
  
    for j in range(low , high): 
  
        # 当前元素小于或等于 pivot 
        if   arr[j] <= pivot: 
          
            i = i+1 
            arr[i],arr[j] = arr[j],arr[i] 
  
    arr[i+1],arr[high] = arr[high],arr[i+1] 
    return ( i+1 ) 
  
 
# arr[] --> 排序数组
# low  --> 起始索引
# high  --> 结束索引
  
# 快速排序函数
def quickSort(arr,low,high): 
    if low < high: 
  
        pi = partition(arr,low,high) 
  
        quickSort(arr, low, pi-1) 
        quickSort(arr, pi+1, high) 
  
arr = [10, 7, 8, 9, 1, 5] 
n = len(arr) 
quickSort(arr,0,n-1) 
print ("排序后的数组:") 
for i in range(n): 
    print ("%d" %arr[i]),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def quick_sort(items, comp=lambda x, y: x <= y):
    items = list(items)[:]
    _quick_sort(items, 0, len(items) - 1, comp)
    return items


def _quick_sort(items, start, end, comp):
    if start < end:
        pos = _partition(items, start, end, comp)
        _quick_sort(items, start, pos - 1, comp)
        _quick_sort(items, pos + 1, end, comp)


def _partition(items, start, end, comp):
    pivot = items[end]
    i = start - 1
    for j in range(start, end):
        if comp(items[j], pivot):
            i += 1
            items[i], items[j] = items[j], items[i]
    items[i + 1], items[end] = items[end], items[i + 1]
    return i + 1

选择排序

  • 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
  • 再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
  • 重复第二步，直到所有元素均排序完毕。
1
2
3
4
5
6
7
8
def select_sort(items, comp=lambda x, y: x < y):
    for i in range(len(items) - 1):
        min_index = i
        for j in range(i + 1, len(items)):
         if comp(items[j], items[min_index]):
                min_index = j
     items[i], items[min_index] = items[min_index], items[i]
    return items

归并排序

  • 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
  • 设定两个指针，最初位置分别为两个已经排序序列的起始位置；
  • 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
  • 重复步骤 3 直到某一指针达到序列尾；
  • 将另一序列剩下的所有元素直接复制到合并序列尾。
1
2
3
4
5
6
7
8
def merge_sort(items, comp=lambda x, y: x <= y):
    """归并排序(分治法)"""
    if len(items) < 2:
        return items
    mid = len(items) // 2
    left = merge_sort(items[:mid], comp)
    right = merge_sort(items[mid:], comp)
    return merge(left, right, comp)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def merge(items1, items2, comp):
"""合并(将两个有序的列表合并成一个有序的列表)"""
    items = []
    index1, index2 = 0, 0
    while index1 < len(items1) and index2 < len(items2):
        if comp(items1[index1], items2[index2]):
            items.append(items1[index1])
            index1 += 1
        else:
        	items.append(items2[index2])
        	index2 += 1
    ## 拷贝item1和items2的保留元素
    items += items1[index1:]
    items += items2[index2:]
    return items

插入排序(Insertion Sort)

  • 将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
  • 从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def insertionSort(arr): 
    #从要排序的列表第二个元素开始比较
    for i in range(1, len(arr)):   
        key = arr[i] 
        j = i-1
    	#从大到小比较，直到比较到第一个元素
        while j >=0 and key < arr[j] : 
                arr[j+1] = arr[j] 
                j -= 1
        arr[j+1] = key 
  
  
arr = [12, 11, 13, 5, 6] 
insertionSort(arr) 
print ("排序后的数组:") 
for i in range(len(arr)): 
    print ("%d" %arr[i])

希尔排序

希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。

希尔排序的基本思想是：先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序（间隔减半），待整个序列中的记录"基本有序"时，再对全体记录进行依次直接插入排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def shellSort(arr): 
  
    n = len(arr)
    gap = int(n/2)
  
    while gap > 0: 
  
        for i in range(gap,n): 
  
            temp = arr[i] 
            j = i 
            while  j >= gap and arr[j-gap] >temp: 
                arr[j] = arr[j-gap] 
                j -= gap 
            arr[j] = temp 
        gap = int(gap/2)
  
arr = [ 12, 34, 54, 2, 3] 
  
n = len(arr) 
print ("排序前:") 
for i in range(n): 
    print(arr[i]), 
  
shellSort(arr) 
  
print ("\n排序后:") 
for i in range(n): 
    print(arr[i]),

堆排序

  • 创建一个堆 H[0……n-1]；
  • 把堆首（最大值）和堆尾互换；
  • 把堆的尺寸缩小 1，并调用 shift_down(0)，目的是把新的数组顶端数据调整到相应位置；
  • 重复步骤 2，直到堆的尺寸为 1。

从列表中找出最大的或最小的N个元素
堆结构(大根堆/小根堆)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import heapq

list1 = [34, 25, 12, 99, 87, 63, 58, 78, 88, 92]
list2 = [
 {'name': 'IBM', 'shares': 100, 'price': 91.1},
{'name': 'AAPL', 'shares': 50, 'price': 543.22},
 {'name': 'FB', 'shares': 200, 'price': 21.09},
{'name': 'HPQ', 'shares': 35, 'price': 31.75},
 {'name': 'YHOO', 'shares': 45, 'price': 16.35},
 {'name': 'ACME', 'shares': 75, 'price': 115.65}
]
print(heapq.nlargest(3, list1))
print(heapq.nsmallest(3, list1))
print(heapq.nlargest(2, list2, key=lambda x: x['price']))
print(heapq.nlargest(2, list2, key=lambda x: x['shares']))
1
2
3
4
[99, 92, 88]
[12, 25, 34]
[{'name': 'AAPL', 'shares': 50, 'price': 543.22}, {'name': 'ACME', 'shares': 75, 'price': 115.65}]
[{'name': 'FB', 'shares': 200, 'price': 21.09}, {'name': 'IBM', 'shares': 100, 'price': 91.1}]

计数排序

  • 花O(n)的时间扫描一下整个序列 A，获取最小值 min 和最大值 max
  • 开辟一块新的空间创建新的数组 B，长度为 ( max - min + 1)
  • 数组 B 中 index 的元素记录的值是 A 中某元素出现的次数
  • 最后输出目标整数序列，具体的逻辑是遍历数组 B，输出相应元素以及对应的个数

桶排序

  • 设置固定数量的空桶。
  • 把数据放到对应的桶中。
  • 对每个不为空的桶中数据进行排序。
  • 拼接不为空的桶中数据，得到结果

基数排序

  • 将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零
  • 从最低位开始，依次进行一次排序
  • 从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列

REFERENCES